Para explicar o que é o desvio padrão, devemos primeiro entender que se trata de uma medida de dispersão que estabelece o grau de agregação de determinados dados de uma amostra ou população coletada. Assim, mantendo uma mesma unidade de observação chega-se ao índice de dispersão de uma medida central.
O desvio padrão indica a variabilidade de dados de uma amostra, podendo ser utilizado para comparações com valores de amostras independentes. Seu objetivo principal é demonstrar qual é a regularidade existente num conjunto de dados, mostrando o grau de oscilação desses dados em comparação com a média dos valores apresentados no conjunto.
Neste artigo vamos trabalhar com o Desvio Padrão baseado no cálculo de População. Vamos aprender primeiro, como funciona o cálculo do desvio padrão fazendo manualmente, para depois apresentarmos a maneira mais fácil de chegar até ele.
Primeiro cálculo do desvio padrão: a média
Vamos trabalhar com um exemplo para tornar mais rápida a compreensão dos passos necessários para se chegar ao desvio padrão.
Numa classe do grau médio temos uma quantidade total de 50 alunos. Não temos necessidade de utilizar todos os alunos para nosso cálculo de desvio padrão. Podemos tomar uma amostra, já que estamos trabalhando com estatística. Vamos, então, de forma aleatória, selecionar 10 deles:
Utilizando a fórmula MÉDIA do Excel, vamos descobrir que esses alunos possuem a idade média de 18,1 anos. Para acessar a fórmula, basta procurar a mesma no assistente de funções, indicando os números que farão parte deste cálculo:
A fórmula MÉDIA automaticamente soma todas as idades e divide o resultado pelo total de dados.
Desvio padrão com base na média
O segundo passo é calcular os desvios ocorridos com base na média obtida. Assim, vamos calcular cada idade subtraindo o valor da média:
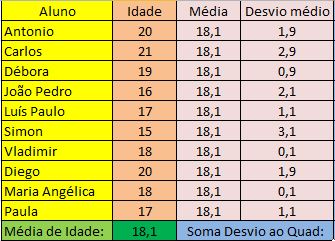
A seguir, vamos calcular o quadrado de cada desvio obtido nesse cálculo. O cálculo é simples: multiplique por ele mesmo cada número de desvio. Logo em seguida, some todos os valores conseguidos na coluna Desvio do Quadrado:
Nosso próximo passo é calcular a média do desvio dos quadrados. Para isso, é só dividir a Soma do Desvio pelo número de alunos da amostra, ou seja, 10:
Chegamos, finalmente, ao cálculo final para saber o desvio padrão existente na amostra dos 10 alunos e suas respectivas idades. Basta, para isso, extrair a raiz quadrada do resultado obtido como Média do Desvio do Quadrado. O assistente de funções também vai ajudar nisso, basta procurar a fórmula RAIZ e indicar o número do qual você precisa para o resultado:
.
Desvio padrão pela fórmula do Excel
O desvio padrão pode ser calculado diretamente pelo Excel, através da fórmula DESVPAD.P Para isso, basta acessar a fórmula de funções, escolher DESVPAD.P, selecionar os valores para o cálculo do desvio padrão e clicar Enter.
.
Como você pode notar, o cálculo da fórmula DESVPAD.P apresenta o mesmo resultado apresentado pelo cálculo manual.
Neste artigo trabalhamos com a fórmula matemática de Desvio Padrão no Excel baseando-se no cálculo de População, existe também o cálculo de desvio padrão baseado em amostras que é o DESVPAD.A (Ou simplesmente DESVPAD em versões do Excel anteriores ao 2010), este também pode ser utilizado e retorna um resultado muito próximo.